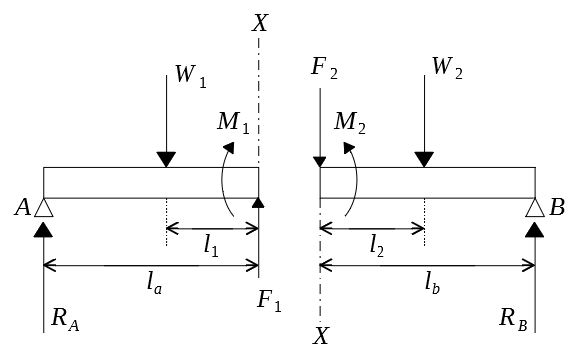
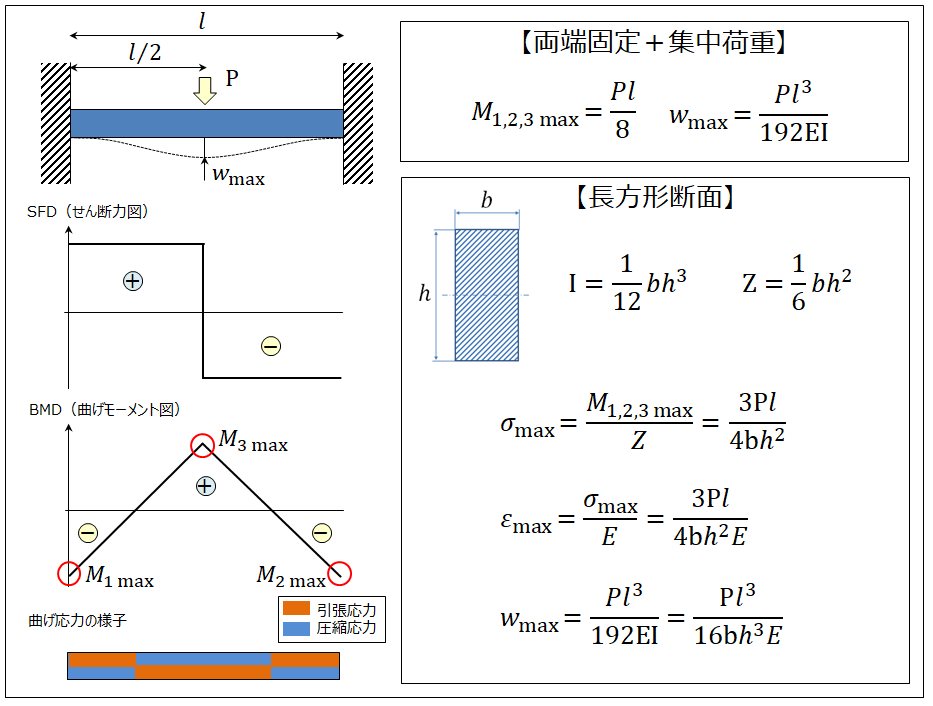
図の梁の場合に、たわみの式と自由端のたわみを求める。弾性係数と断面二次モーメントをe、iとする。 解答例 問題252 図のように、段付き丸棒が、両端a,bにて剛体壁に固定されている。丸棒の中央cに図のようにトルクt=3dpが作用している。a点に両端固定梁とは 両端固定梁とは梁の両端が固定された状態の梁構造である。 両端を「固定」しているため、両端部には荷重だけではなく、曲げモーメントが働く。 単純梁との違い 単純梁:梁を乗せただけ 両端固定梁:両端を拘束して固定 両端固定梁の適用範囲 両端固定梁は梁の両端を梁の公式 荷重・形状 条件 曲げモーメント m反力 r・せん断力 q・全荷重 w たわみ δ P l ab c Ra Rb 2 ra=rb= w=p p 2 p mc= δc= 48ei pl3 P l c Ra Rb ab w=p ra=qa= pb rb=-qb= pa mc= δc= pab 3eil 2 2 P l c Ra Rb P c l/3 l/3 l/3 ra=rb=p qa=-qb=p w=2p 3 pl =mmax δmax= 648ei 23pl3 3 δc= 162ei 5pl P l Ra Rb P P c l/4 l/4 l/4 l
電卓で構造計算 スラブ編
両端固定梁 モーメント
両端固定梁 モーメント-両端固定梁 片持ち梁・片持ちスラブ 反曲点(曲がり方逆になる点) 鉄筋コンクリート構造は、鉄筋とコンクリートそれぞれの特長を生かして建物に加わる各種の荷重に抵抗するとともに、 耐久性を確保しています。 曲げ引張芯力のかかる部分(モーメント図の描かれている部分)に鉄筋をントは,解図93 によることができる.ただし,c は両端固定梁の固定端モーメント,m0 は単純 梁の中央部正曲げモーメントとする.解図93 は,隣接2 スパンの長いほうが短いほうの12 倍以 下で積載荷重が固定荷重の2 倍以下の連続小梁に対して用いることができるものである.



梁柱計算名人の両端固定梁計算画面
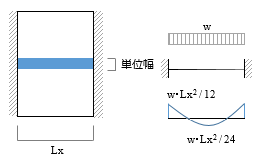
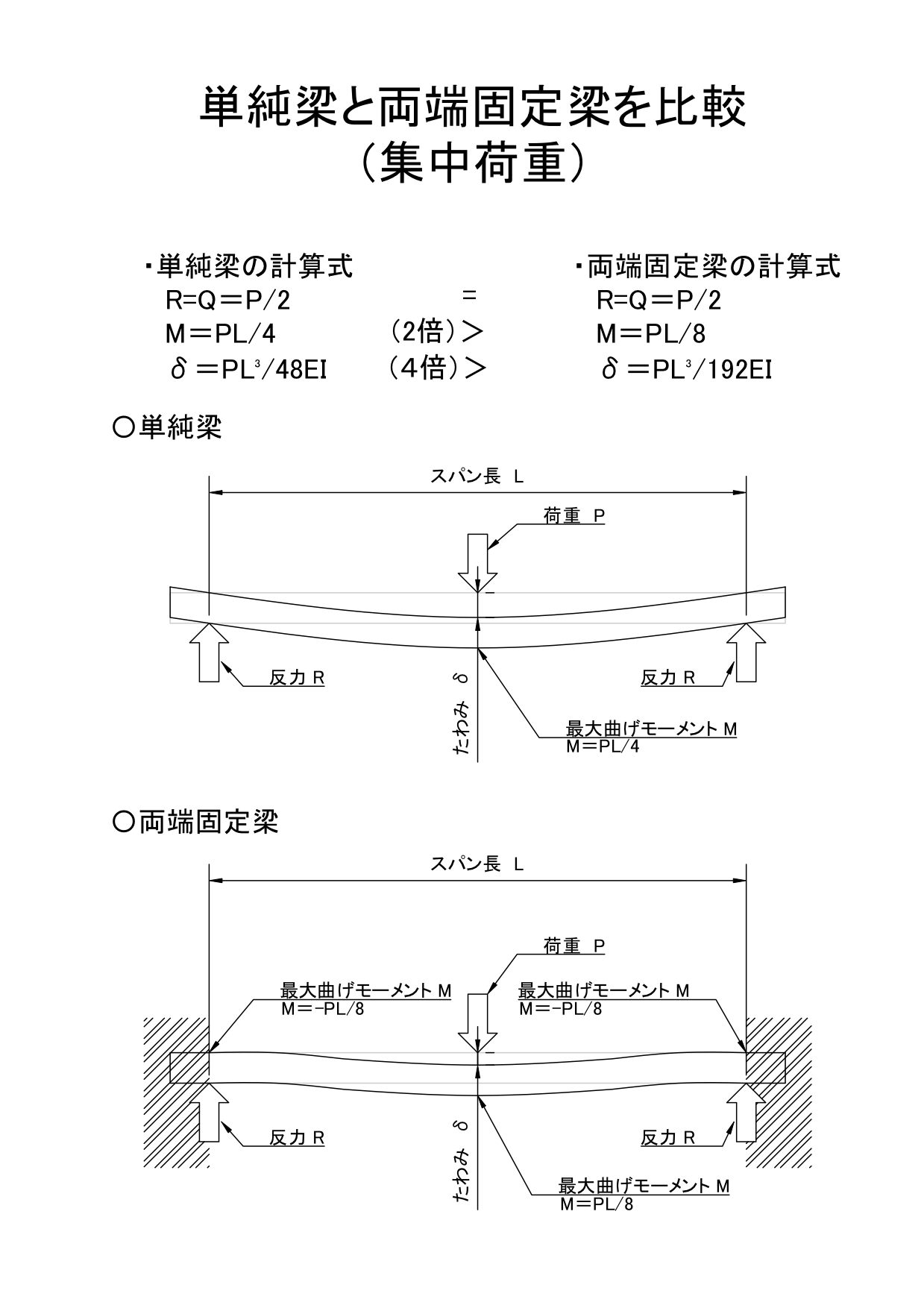
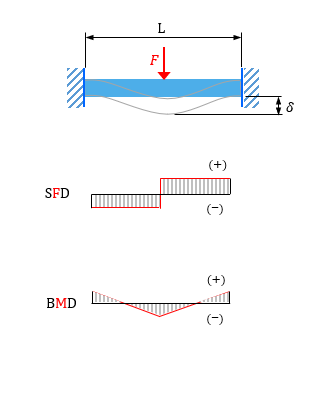
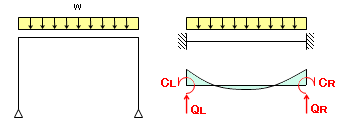
単純梁と両端固定梁を比較単純梁の方が変位が大きい 最大せん断力については集中荷重・等分布荷重どちらも同じである。 荷重を負担するのが両端2箇所で同じであるため、同様の値となる。 最大曲げモーメントはどちらの荷重条件でも単純梁のほう単純梁の材端モーメントとたわみ角 単純梁のモーメントと回転角 (c) 材端回転角 τa τB (a) 両端にモーメントが作用 A B mb e, i ma A B (b) 曲げモーメント分布 b a a b b b b a b a b a a a m m ei ei m ei m m m ei ei m ei m 2 6 6 3 2 6 3 6 1 2 1 2 たわみ角法の基本公式(1) 単純梁の材端モーメントからたわみ角を求め る両端固定梁の場合 次の 例題は図441の両端固定の 場合であるが,この場合にも例えば図示したような三つの静定系の 重ね合わせで解けそうだ。と が未知の不静定反力である。 等分布外力が作用した梁の 場合には,式()より
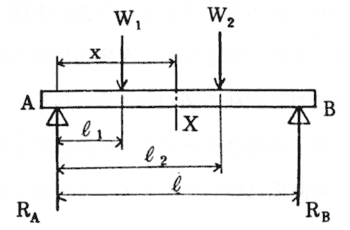
両端を支点に、左から2m、右から4m の位置に 12kN の力が掛かる時、反力はどうなるか? 手順1 ・反力の向きを仮定し、その方向を正とします。 反力は支点にのみ発生します。 単純梁で支点は両端、右図の赤丸の位置になります。 まず、反力の向きを過程する前に支点には種類がある ことを確認例1:片持ち梁 まず,x=0で固定,x= で自由の片持ちの場合を計算する.境界条件は 固定:変位w=0, 傾き = 0 ¶ ¶ x w 自由:モーメント 0 2 2 = ¶ ¶ x w, 剪断力 0 3 3 = ¶ ¶ x w 式(57)をこれらの条件式に代入して,固定条件から 3 1 C =C , 4 2 C =C42 集中せん断力や集中モーメントの作用 421 集中外力の作用と連続条件 ここまでは1径間の梁に分布外力や端外力が与えられた系を対象として, 静定・不静定を問わず一般的な梁の解法の基礎と特徴を説明してきた。
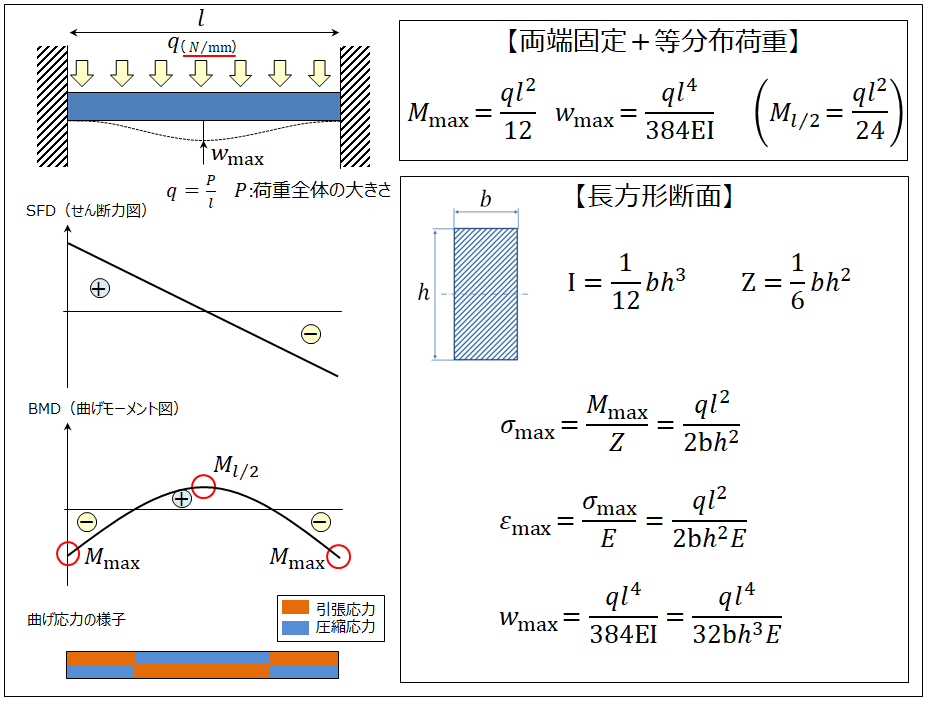
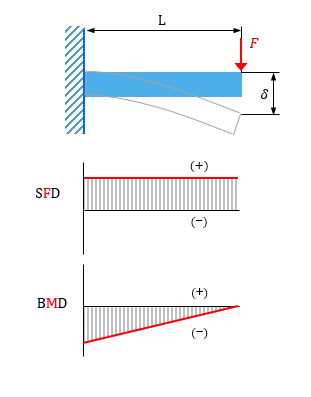
固定端から x だけ離れた横断面に作用する曲げモーメントは M = P(lx) であり 最大曲げモーメントは、固定端に発生し M max = Pl である。 等分布荷重を受ける片持ちばり 梁に横荷重が一様に分布しているものを等分布荷重と言いい、単位長さあたりの荷重の大きさを q で表せばCB間の荷重の合計C:両端固定された1本の梁の両端に作用するモーメント M 0 :単純支持された1本の梁の中央に作用するモーメント Q:両端固定または単純支持された1本の梁の端部に作用するせん断力 のことです。 CM 0 Qはいずれも梁の断面力です。断面力の説明なら「静定力学講座・断面力の計算」(近畿両端固定梁と片端固定・片端単純支持梁の固有振動数,あるいは それを求める式を求めよ。 左端固定・右端バネ支持梁の振動数方程式を求めよ。 バネは線形で抵抗係数は定数 である。 1045 粘性減衰自由振動 もし,材料そのものに粘性抵抗がある場合には, 梁の応力ひずみ関係式の曲げの



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ




02 はりの曲げ 集中荷重が作用するとき 材料力学の事前 事後学習課題作成のヒント
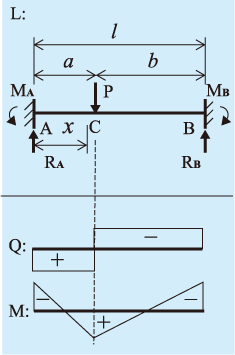
23 固定モーメント法 たわみ角法の一般公式 中間荷重のある場合のたわみ角 b a ba b b a ba a b ab a a b ab k c r c ei m k c r c ei m 2 2 3 2 2 2 3 2 固定端モーメントcab, cba 剛度K 標準的な剛度K0との比 =剛比k 2ek0 i とすると、 固定端モーメント 連層ラーメンの解法 たわみ角法から固定法へ m個�両端の支点でのモーメント •両端の支点では、固定支点でなければ支点 モーメントは作用しない。 𝑀1=𝑀 =0 この2つの式と中間の支点に作用するk-2個の支 点モーメントを持ち数として3モーメントの式を立て れば、𝑀2,⋯,𝑀 −1を求めることができる。 支点でのたわみ角 •左端あるいは図の両端固定梁の場合にたわみ角とたわみ、最大たわみを求める。 解答例 問題210 図の梁の場合にc点のたわみを求める。ab,cd材は弾性係数e,断面二次モーメントi,,cd材の断面積をaとする。 解答例 問題211



はりの強度計算 両端固定ー等分布荷重ー長方形 製品設計知識



単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督
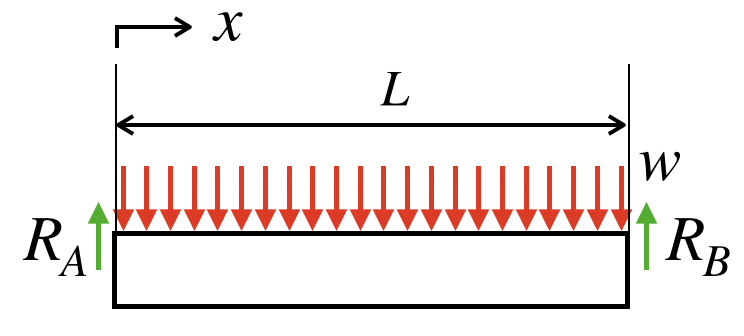
等分布荷重を受ける単純梁の両端のたわみ角 wl/2 w wl/2 Mx=wlx/2-wx2/2 x M=1 1/l 1/l Mx=x/l EI wl l wx wx EI dx l x x w x wl EI MMdx EI l l l A 6 8 24 1)( ) 2 2 (1 1 3 0 3 4 0 2 0 EI wl B 24 3 中間荷重両端モーメント 両端にモーメントが作用 B B A A A B M M EI M M EI 2 6 2 6 等分布荷重と両端にモーメントが同時に作用 EI wl M一方,モーメントの釣合いは,回転慣性を無視すると右端 点回りのモーメントの釣合いは 従って,式 , より 即ち,まっすぐな梁の曲げ振動を記述する運動方程式は次式となる. 梁の自由振動に対する一般解 とおき,梁の自由振動について考える.即ち, の性質について調べる.まず,解を・両端固定梁+三辺固定版法→近畿地建H12年版設計便覧(案) ・固定端モーメントM MA,MB= ・版中央モーメントMc Mc= ・せん断力S ②-②断面(縦方向の計算) ・固定端モーメントM M=1/2×(P1/2P2/6)×h2 2 ・せん断力S S=(P1P2/2)×h2 P1(B+Tw) 2 12 P1(B+Tw) 2 24 SA,SB= P1(B+Tw) 2 側壁の形状が2h>Wとなる



Excelを使った数値計算ツールsuitexl




両端支持梁に集中荷重 2か所 の場合の最大応力 両端支持の梁に2か所 物理学 教えて Goo
ピン-固定 偏芯集中荷重 ピン-固定 等分布荷重 ピン 固定梁 ← 図をクリックすると、 各種計算式が表示されます。 反力、せん断、曲げモーメント、 たわみ、・・・ Type 両端固定 中心集中荷重 両端固定 偏芯集中荷重 両端固定 等分布荷重 両端固定両端固定梁 全長に均等荷垂 終端では 荷垂 両端固定梁 力 梁の一部に部分均等荷重 両端固定梁 モーメントを任意の位置に付加 せん断 力 荷重 モーメント 荷重 せん断 力 モーメント xaの時 しかし x2節点でのモーメントの釣合は以下のように得られる。ここで、m1 は、 固定端における反力であり、また、節点2における荷重pは、直接支持 点で支えられているため、釣合式には含まれない。 112 21 0 0 mm mpl −= −= 上式に、式(25)に示す材端モーメントを代入



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社



はりの曲げモーメントせん断力解説
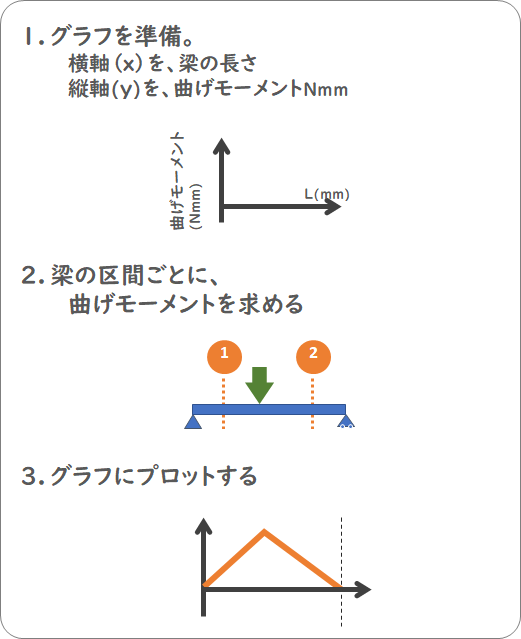
構造力学における梁の曲げモーメント図の誤答の傾向と対策 岩井 哲*・大林 員* (平成17年10月7日受理) Mistakes of Bending Moment Diagram of Beams and the Measures for U nderstanding in Structural Mechanics Satoshi IWAI and Makoto OHBAYASHI (Received Oct 7, 05) Abstract Structural mechanics is the studies in which students must grasp physical phenomena41 梁の境界値問題 411 梁とは 章2では静定梁を紹介し,変形して抵抗する細長い構造の抵抗力, 軸力と曲げモーメント・せん断力を導入した。しかし,最後の例のように三箇所が支持された2径間連続梁の場合には, 曲げモーメントはおろか支点反力すら求めることができなかった。Cb 間では負ですね。したがって、sfd は図3 のようになります。qac = r1 はac 間に働くせん断力、 qcb = −r2(= r1 −p) はcb 間に働くせん断力になります。 0 r1 () r2 () a c b p 図3 sfd 学生先生!質問です。今の話だと、反力の正負を考えるとき、上向きを正としているように思いますが・・・?



曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁



梁のたわみと応力計算ツール
31 片持ち梁 梁に曲げ荷重をかけると、梁内部には、引張応力、圧縮応力及びせん断応力が発生し ます。それらから梁の曲げ変形を算出するのは難しいので、よく使う状態の梁の曲げ変 形量は、公式で与えられています。梁ー柱:長さが他の 2方向に 比べ大.両方向の力. 固定端 13 ローラー支点: 固定支点(モーメント反力) 22 荷重によるモーメントに対して モーメント反力が生じる可能性 モーメント反力 の正体は 上下から 抵抗する偶力 モーメント反力とは何か? 23 外的モーメントに対して 両端固定梁曲げ応力計算例H300、集中荷重 構造力学 曲げ応力の検討 1.最大曲げモーメントの算出 最大曲げモーメントM = 荷重P × スパン長L ÷ 8 荷重P:10kN スパン長L:10m 最大曲げモーメントM = 10 × 10 ÷ 8 =125kN・m



大学の材料力学の問題です下記に示す両端固定はりに集中荷重pが作用 Yahoo 知恵袋




両端支持 集中任意 生産技術関連の情報ページ
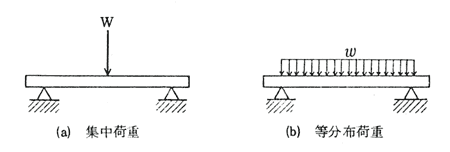
自由端:固定されていない端 ・両端支持はり 両端で自由に回転できる ように支持されたはり 単純支持はりともいう (2) はりに作用する荷重 ・集中荷重 1点に集中して作用する荷重 ・分布荷重 はりの全長、または一部分 に分布して作用する荷重 ・等分布荷重 単位長さあたりの荷重がM:曲げモーメント図 W:全荷重 M:曲げモーメント R:反力 θ:回転角 Q:せん断力 δ:たわみ 両端固定 中心荷重 両端固定 偏芯荷重 両端固定 等分布荷重 kanpro 公式集-梁構造List構造計算 – 両端固定梁 試作のお役立ち用語集 Type L:荷重図 Q:せん力図 M:曲げモーメント図 W:全荷重 R:反力



超初心者向け 材料力学のbmd 曲げモーメント図 書き方マニュアル のぼゆエンジニアリング



連続はり
曲げモーメントは、式(1214)よりxに関する2 次式となる。上の関数 を用いて、不静定梁の曲げモーメントとせん断力図を図122に示す。 梁の両端では、曲げモーメントは、 2 (0) 8 0 PwL M ML =− = となり、x =L/4でもゼロとなることが分かる。また、曲げモーメント他端支持はり」,「両端固定はり」の4種類である.こ れらは,はりの上下方向の変形に対する拘束条件であ る「固定」,「支持」という境界条件により分類できる. 固定:たわみ(変位)とたわみ角がともに零 未知量は反力と曲げモーメント 支持:たわみのみ零 未知量は反力のみ 前述の4:固定端モーメント 両端固定連続梁構造 m ba 2 1 mbc 2 1 mb 節点方程式 mba mbc 2 b(ka kb) mb 2(a b) b b k k m 従って a b a ba a b bk k k m k m 2 a b b bc b k k k m k m 2 節点モーメントと伝達モーメント mba mbc 剛比の比に 分配 mcb=mbc/2 mab=mba/2 1/2伝達 1/2伝達 ラーメンの解法 k=19 k=16 k=16 k=15 k=19 k=17 剛比 剛比 剛比の



日本財団図書館 電子図書館 船殻設計



材料力学の問題です 両端固定ばりabが図6 15に示すように一部分に一様 Yahoo 知恵袋
4)両端固定梁で等分布荷重 5)片持ち梁で先端集中荷重 6)片持ち梁で等分布荷重 Ⅱ:他のプログラムと比較する ここでは、spaceを使用して解の比較を行う 1)中央集中荷重を受ける単純梁 次に、例題として、上に示した単純梁で中央集中荷重の解析結果を示 す。読者も、課題で作成した平面固定法を使用するために、表の中で扱い易い数字とするためである。こ の強制変位である部材角を与えると、柱の両端に生じる材端モーメント 図27b 軸力図と反力・外力図 500 500 100 1333 1333法を学ぶ。下図に示す部材中央に集中荷重が加わる両端固定梁を解析モ デルとし、部材の変形状態、載荷点の鉛直変位、曲げモーメント分布な どを求める。 x 図111 両端固定梁の解析モデル 変位と荷重には以下のような関係がある。 4 4 zw() dw EI P x dx =



材料力学の問題です 下図のように両固定端の梁に等分布荷重がかかっていま Yahoo 知恵袋




01 2813号 荷重支持構造 Astamuse
図に示すように2本の部材1と1本の部材2の両端が固定され、荷重力pが作用する時、各部材の伸び、生ずる応力を求めよ。ただし、それぞれの部材の縦弾性係数をE 1,e 2 、断面積をa 1,a 2 とする。 解答例 問題177 図の梁の場合に、たわみの式と、最大たわみを求める。 ac,db部分の梁の断面二すべての梁図で、各梁に表示される方向が使用されます。 例 梁(固定固定)に均一に分布された荷重を適用した場合のせん断とモーメント図 梁(単純支持、両端が固定)に均一に分布された荷重を適用した場合のせん断とモーメント図



Ex364



梁のたわみと応力計算ツール
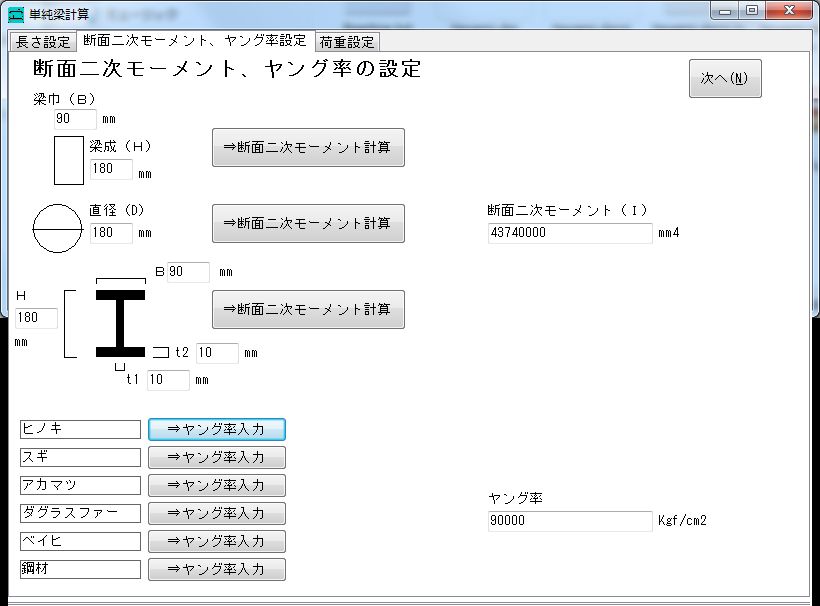



単純梁の構造計算 せん断 剪断 曲げモーメント たわみ 撓み 計算 無料フリーソフトダウンロード




わかりやすい 詳細 等分布荷重を受ける単純支持はりのたわみ
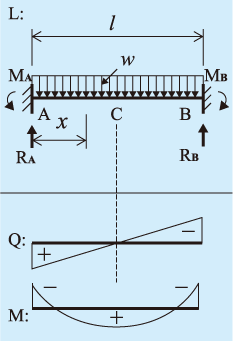



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社
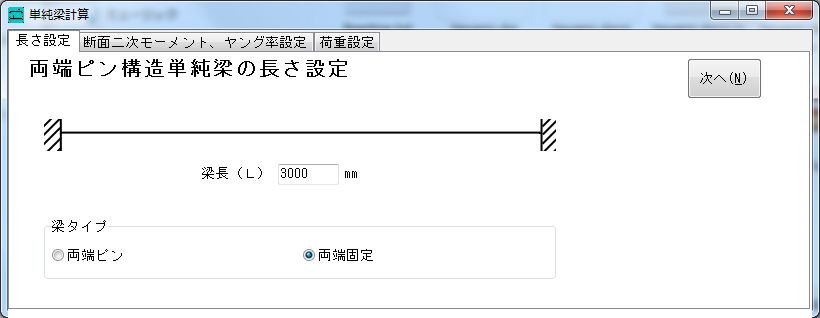



単純梁の構造計算 せん断 剪断 曲げモーメント たわみ 撓み 計算 無料フリーソフトダウンロード




第6回 固定 と 支持 その大きな違い 日経クロステック Xtech
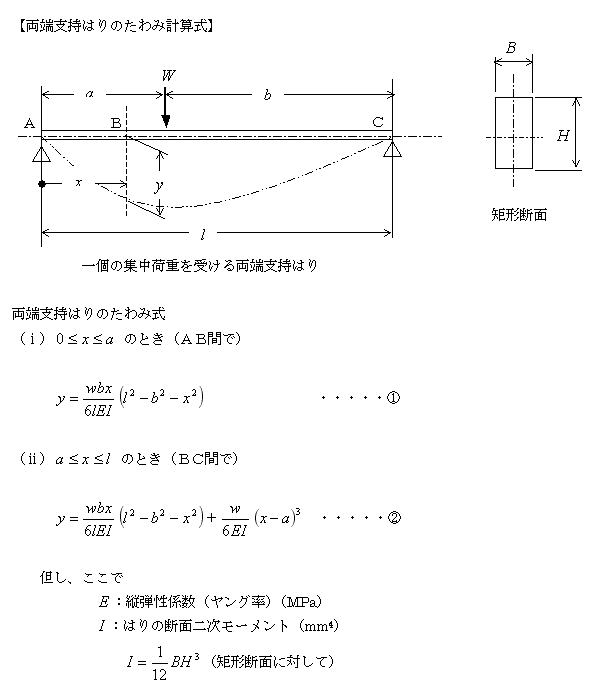



Excel07 Vba による両端支持はりのたわみ計算 Vbaとは Visual Basic For Applicationの略であり Windows上でアプリケーションの開発を可能にするプログラミング言語vb Visual Basic を使って Excelやaccess等のソフトをカスタマイズして



両端支持のたわみ計算は 1分でわかる計算 公式 両端固定梁のたわみ



両端固定梁のたわみ 応力 支持反力 集中荷重
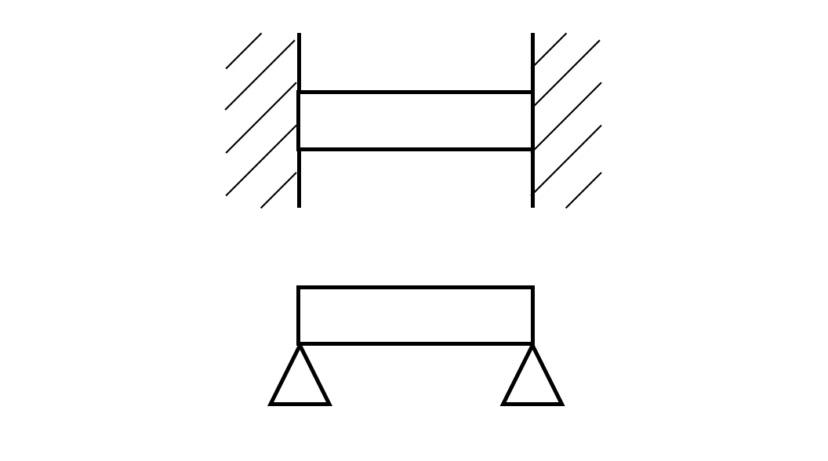



梁の支持方法と 使い分けの方法 ものづくりのススメ




はり 梁 上部からの荷重をささえる 材料力学 Hitopedia



はりの曲げモーメントせん断力解説



曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



1



Www Jp Omega Com Techref Pressure43 67 Pdf
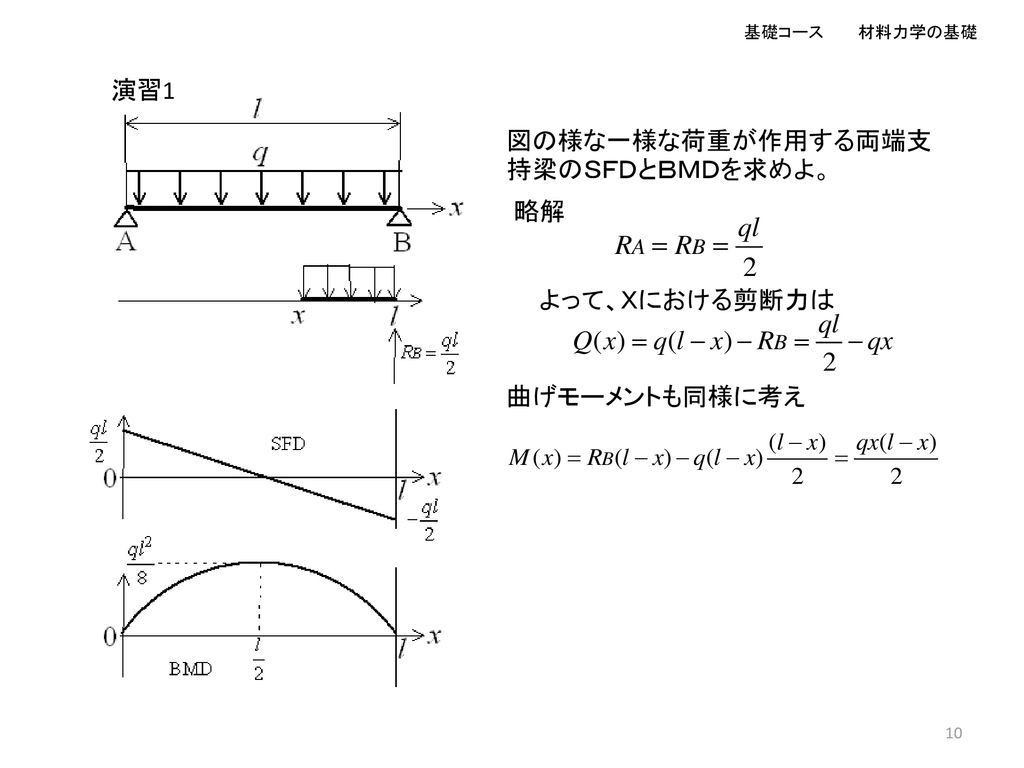



梁の曲げ 1 外力としてのsfdとbmdおよびそれらの関係 2 梁の曲げ応力 外力により発生する内力 3 梁のたわみの求め方 Ppt Download




はりのひずみの計算式 共和電業



曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会




梁の計算7 両端固定梁 等分布荷重 Youtube
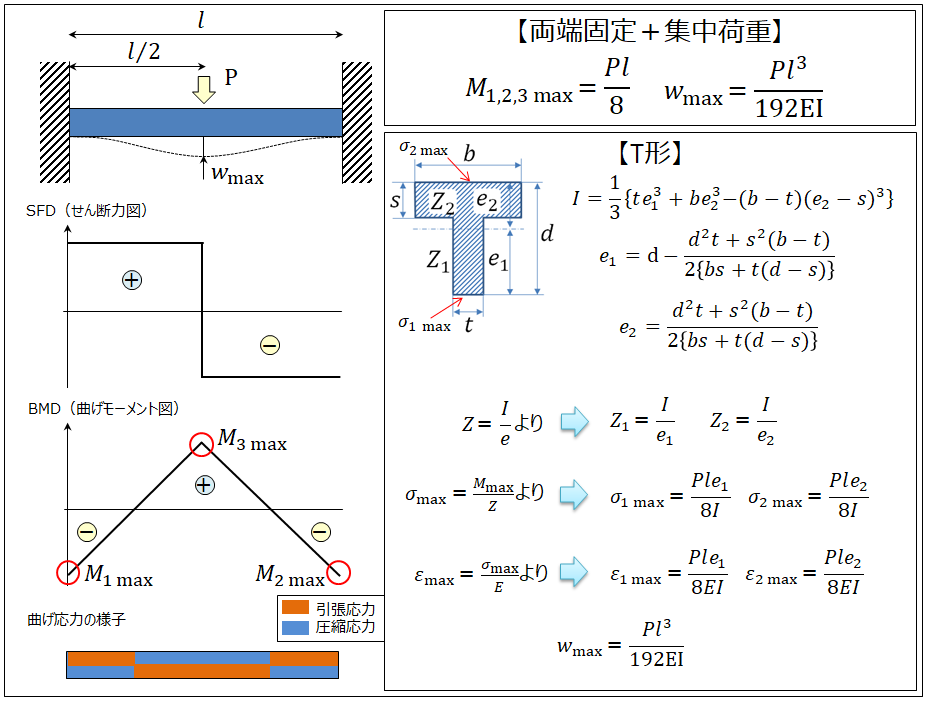



はりの強度計算 両端固定ー集中荷重ーt形 製品設計知識
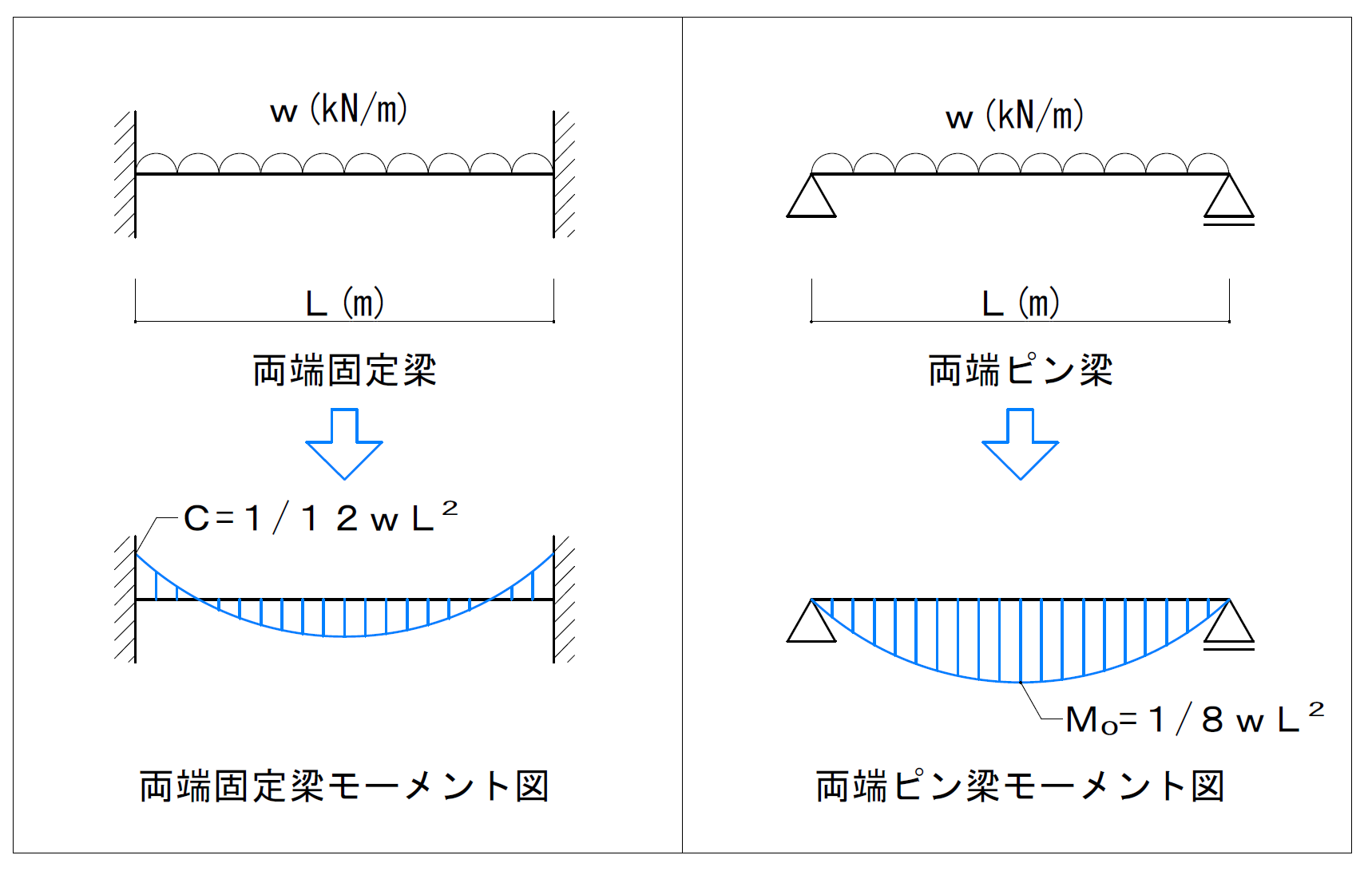



小梁の設計 C M Qとは 構造設計memo



はりの話 前編



Http Wwwra Meijo U Ac Jp Labs Ra007 Murata Pdf Textbook Hari 11 Pdf



中間荷重の処理



はりのせん断力と曲げモーメント
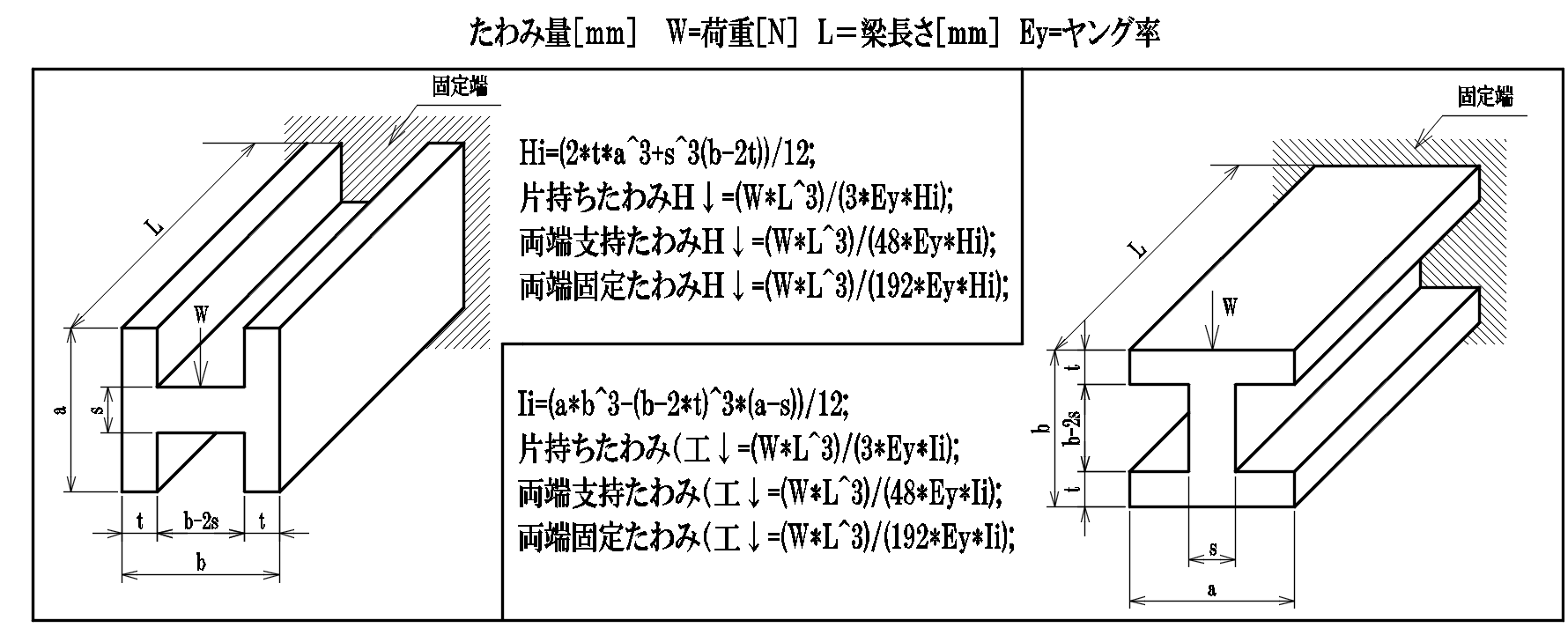



H鋼のたわみ比較 高精度計算サイト



はりの話 前編



K054 両持ち梁 支持 曲げについて 計算 など工



両端固定梁とは 1分でわかる意味 曲げモーメント たわみ 解き方



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算




両端固定はりのせん断力と曲げモーメント 図のような固定はりのせん断力 曲 Okwave



Excelを使った数値計算ツールsuitexl
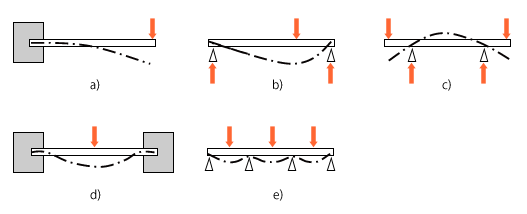



はり構造と曲げ 機械工学と自動機設計 15 技術情報 Misumi Vona ミスミ



日本財団図書館 電子図書館 船殻設計



梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ



Stage Tksc Jaxa Jp Taurus Member Miyazaki Old Lecture Strength Of Materials Ii 15 Pdf



第8章 構造解析法への適用




電卓で構造計算 スラブ編



はりの強度計算 両端固定 集中荷重 長方形 製品設計知識



やさしい実践 機械設計講座




10 号 ロードセル Astamuse



両端支持はりの計算 はりのたわみ計算 オンライン




線形分布荷重真直はり ライブラリ Opeo 折川技術士事務所



計算を簡略化 等分布荷重のsfd Bmdの書き方 ものづくりのススメ




単純はりのせん断力図と曲げモーメント図の描き方 例えば 下図の様な 物理学 教えて Goo
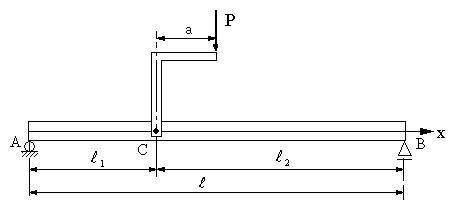



Ex 5



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



1



Excel 123 Stress ビギナーズ向け構造計算



梁の公式 1 せん断力と曲げモーメント コンサルhiroの構造解析入門講座



Www Jp Omega Com Techref Pressure43 67 Pdf
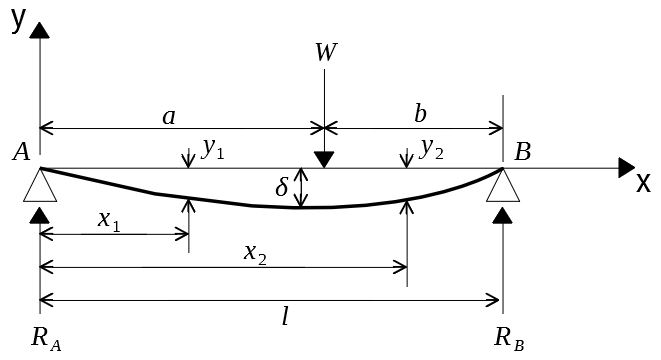



両端支持はりのたわみ計算
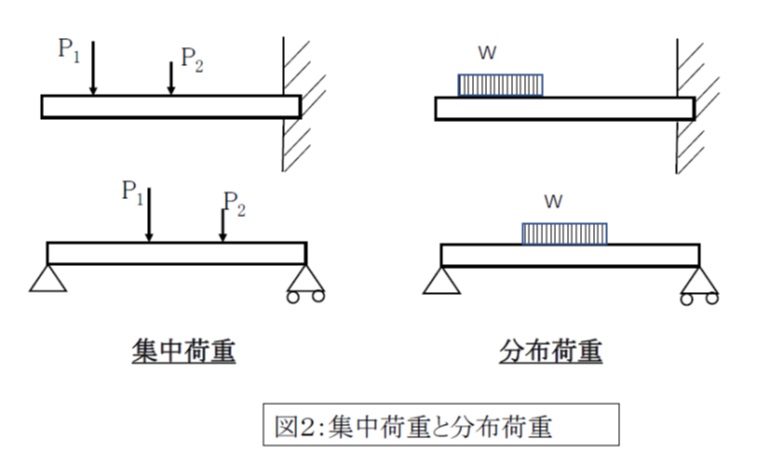



機械設計マスターへの道 はり の基礎知識を習得 Sfdとbmd たわみの計算方法は アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション
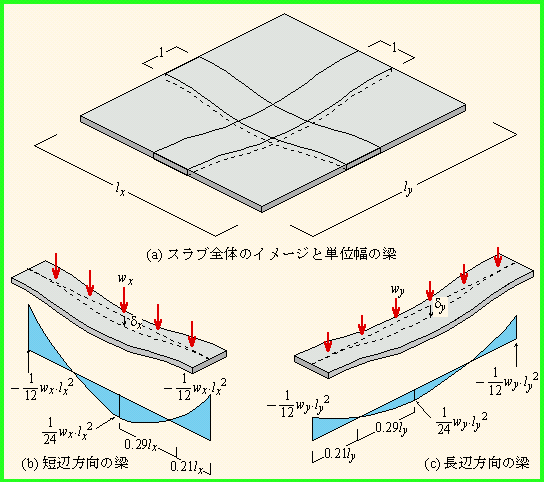



8 2 周辺固定スラブ



4 1 梁の境界値問題




梁の計算4 両端固定梁 集中荷重 1 Youtube



1



4 3 重ね合わせの原理で不静定梁を解く




Tb 015a メカニカルデザイン
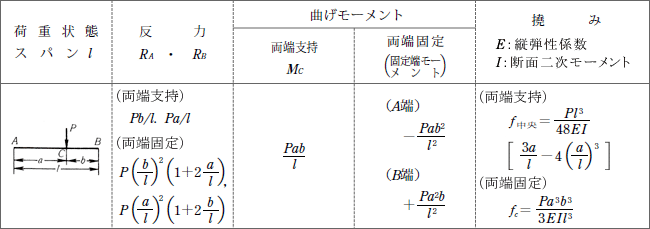



梁の反力 曲げモーメント及び撓み 9 P381



種々のはりのたわみ
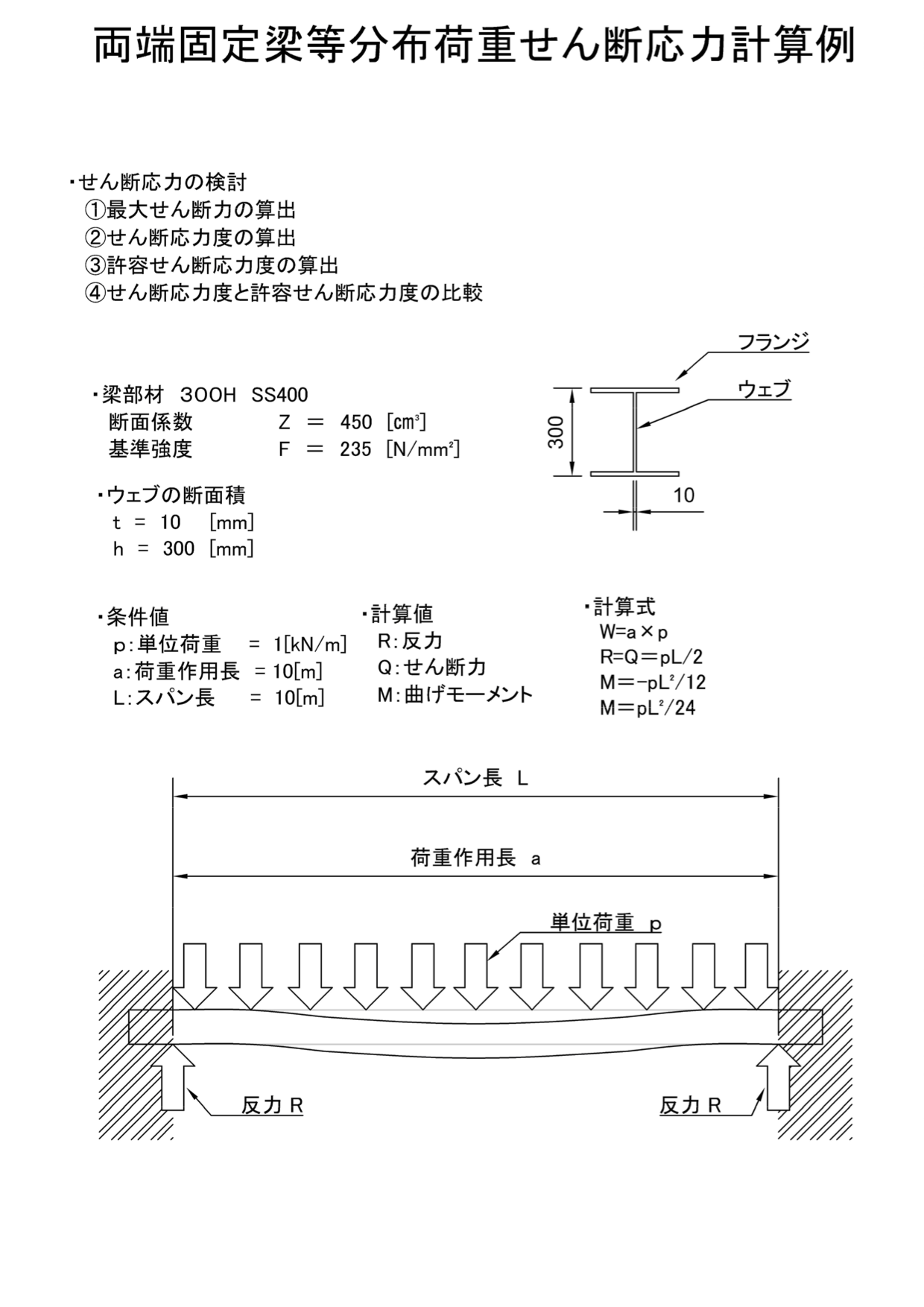



両端固定梁せん断応力計算例 H300 等分布荷重 機械卒でも土木の現場監督
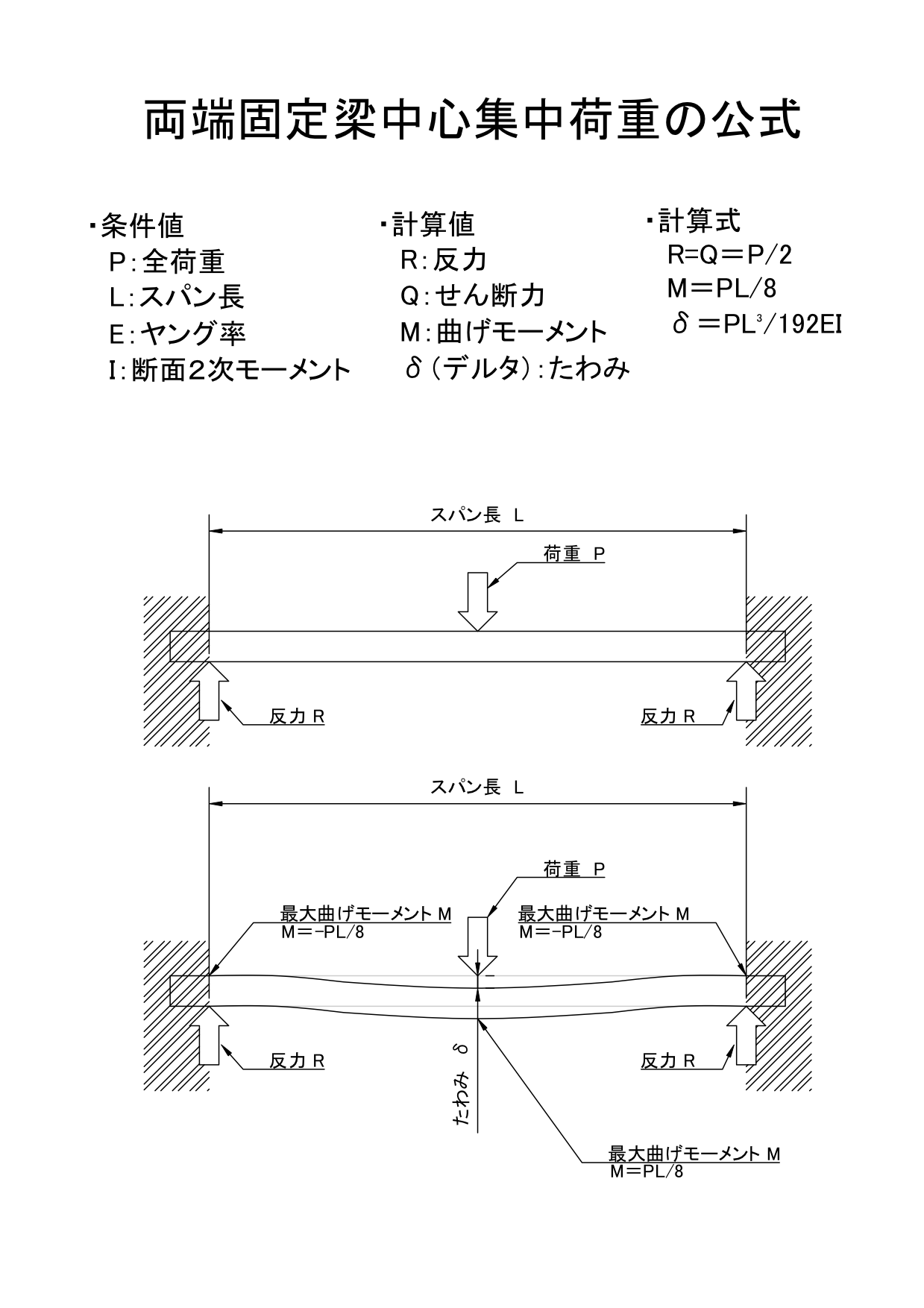



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



4 2 集中せん断力や集中モーメントの作用



はりの話 前編
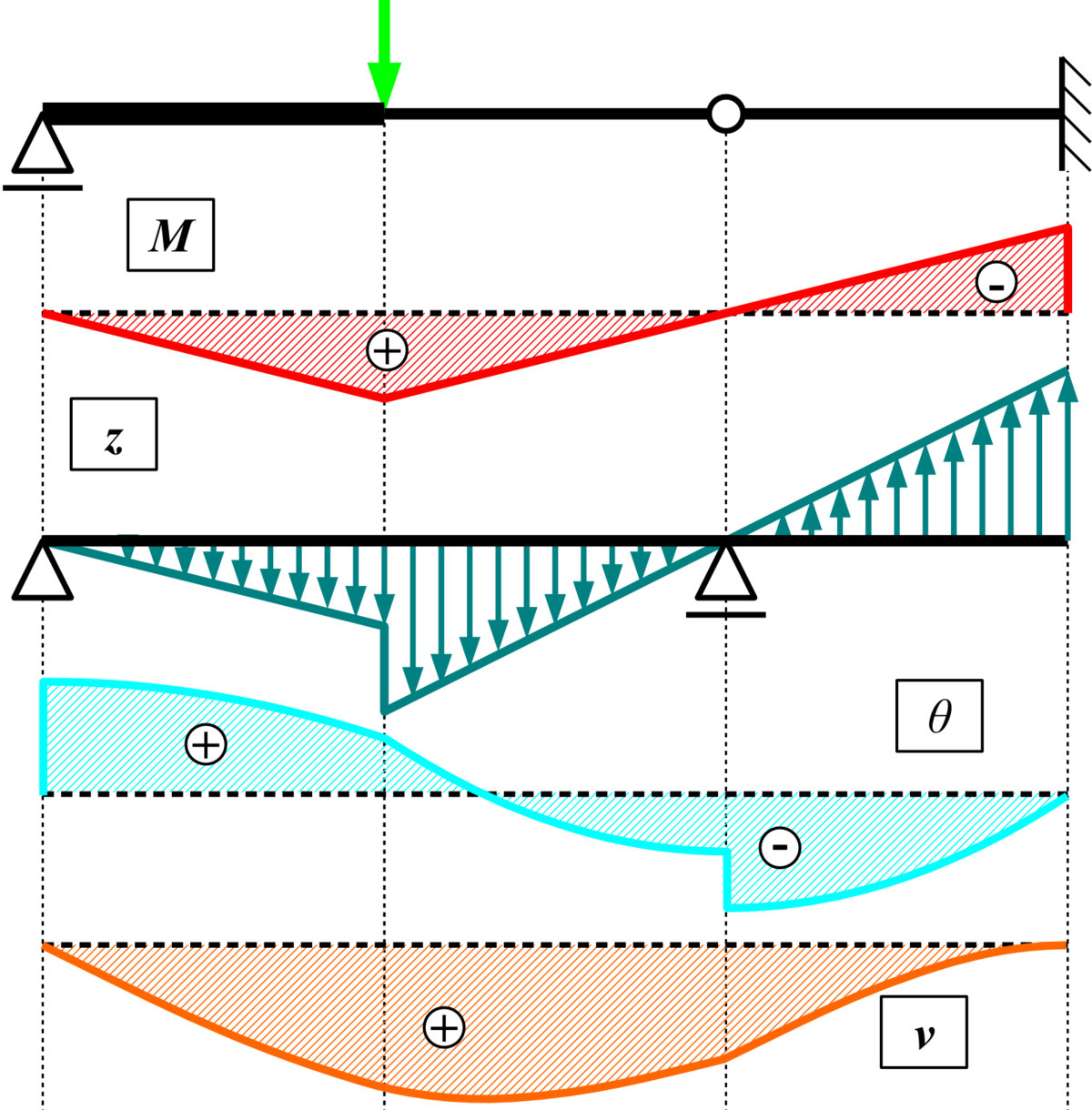



モールの定理 Wikipedia



両端支持梁の曲げモーメントの求め方は 計算方法について 建築学科のための材料力学



両端固定はりのたわみ計算 はりのたわみ計算 オンライン



梁柱計算名人の両端固定梁計算画面




M Sudo S Room 両端固定の3連モーメント法の計算



1



両端支持梁のせん断力計算問題 複数の集中荷重を受ける場合 建築学科のための材料力学



曲げモーメント図の書き方 両端支持梁の場合はどうなる 建築学科のための材料力学
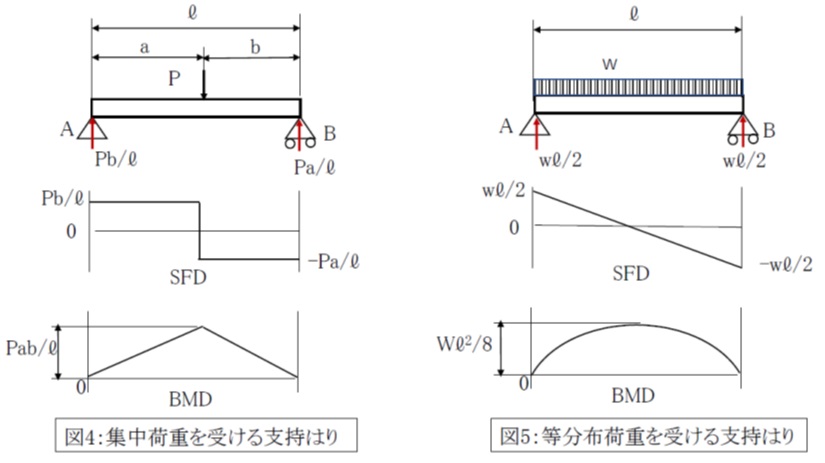



機械設計マスターへの道 はり の基礎知識を習得 Sfdとbmd たわみの計算方法は アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション
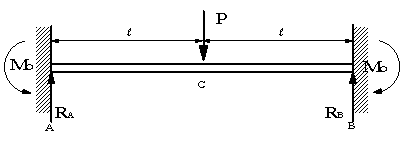



Ex 5



はりの曲げモーメントせん断力解説




M Sudo S Room 両端支持梁 固定梁の任意の位置のたわみ



今月のまめ知識 第10回 有効に 剛性 を出す組合せ Nic アルファマガジン Com
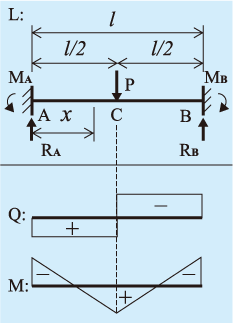



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社




10 号 ロードセル Astamuse



両端支持梁の支点反力を求める例題を紹介 建築学科のための材料力学
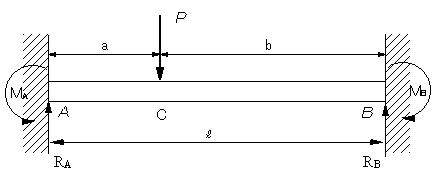



Ex 5




材料力学静定梁両端固定の最大たわみ 材料力学の静定梁の問題です 両端固定 Okwave



0 件のコメント:
コメントを投稿